ソートアルゴリズム一覧(バブルソート・クイックソート・マージソート・選択ソート・挿入ソート・ヒープソート)について
ソートアルゴリズムの種類は以下のように8種類以上あります。
- バブルソート
- クイックソート
- マージソート
- 選択ソート
- 挿入ソート
- ヒープソート
- シェルソート
- 基数ソート
バブルソート
バブルソート(基本交換法)は、データ列中の隣り合った要素同士を比較し、順序が合っていなれば交換する操作を繰り返して整列するアルゴリズムです。
1回の操作ごとに、未整列データのうち最大値または最小値が確定していきます。
バブルソートを流れ図で示すと次のようになる。
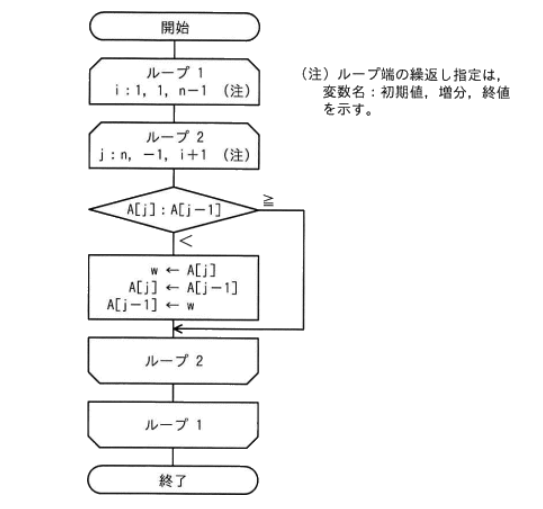
クイックソート
クイックソートは、整列対象のデータ群をある基準値以下のグループと基準値以上のグループに分割し、さらに分割後の各グループで基準値を選んでグループに分割するという処理を繰り返してデータを整列するアルゴリズムです。※分割統治型の整列アルゴリズム
例:配列に格納されたデータ2,3,5,4,1をクイックソートにて整列する場合
基準値:配列の左端の値、分割は基準値よりも小さい値と大きい値に分ける
①[2,3,5,4,1]
②左端の2より小さいグループ、大きいグループに分ける(1回目の分割)
[1],[2],[3,5,4]
③各グループで左端の値を基準に小さいグループ、大きいグループに分ける(2回目の分割)
[1],[2],[3],[5,4]
④各グループで左端の値を基準に小さいグループ、大きいグループに分ける(3回目の分割)
[1],[2],[3],[4],[5]
マージソート
マージソートは、マージ(merge)とは、2つのソート済データを併合(マージ)することで1つのソート済データを取得する処理をさします。マージソートでは再帰的な呼び出しにより、十分に小さく分割してからそれを統合(マージ)します。分割統治法と呼ばれる手法です。
選択ソート
選択ソートとは、対象データから最小値(最大値)を選択・交換を繰り返すことでソートを行います。
隣り合う要素を交換するバブルソートと比較し、最小値(最大値)の交換を繰り返す選択ソートは、データの交換回数一定して少なくなります。よってバブルソートよりは高速になります。
挿入ソート
挿入ソートは、未整列部分の先頭から要素を取り出し、取り出した要素を整列済み部分の順序関係を保つよう挿入することを繰り返して整列するアルゴリズムです。
ヒープソート
ヒープソートは、未整列の部分を順序木にし,そこから最小値を取り出して整列済の部分に移す。この操作を繰り返して,未整列の部分を縮めていく方法です。
シェルソート
シェルソートはある間隔おきに取り出した要素から成る部分列をそれぞれ整列し,更に間隔を詰めて同様の操作を行い,間隔が1になるまでこれを繰り返す。
シェルソートによる整列具体例
データ列 7,2,8,3,1,9,4,5,6 を手順(1)~(4)に従って整列する
(1)”H←[データ数÷3]”とする。
(2)データ列を,互いにH要素分だけ離れた要素の集まりからなる部分列とし,それぞれの部分列を,挿入法を用いて整列する。
(3)”H←[H÷3]”とする。
(4)Hが0であればデータ列の整列は完了し,0でなければ(2)に戻る。
// 実施結果 H ← 9÷3 //H=3 Hが3なので、要素ごとが互いに3つずつ離れた要素から成る3つの部分文字列に分解し、それぞれ整列 H ← 3÷3 //H=1、(3)の処理1回目 Hが0ではないので、(2)の処理に戻る Hが1なので、要素ごとが互いに1つずつ離れた要素から成る 3,1,6,4,2,8,7,5,9 を整列し、 1,2,3,4,5,6,7,8,9 とする。 H ← 1÷3 //H=0、(3)の処理2回目 Hが0なので、データ列の整列が完了



コメントを残す